Diversifizierung beim Ankauf von Erneuerbaren Energien-Portfolien

Aktuelle Marktsituation

Der An- und Verkauf von Assets im Bereich der Erneuerbaren Energien (EE) ist ein wichtiges Standbein der Branche. Zum einen wird Projektentwicklern, durch den Verkauf ihrer projektierten Wind- und PV-Parks, ermöglicht frisches Kapital für weitere Projekte einzuholen, ohne diese Parks selbst betreiben und viele Jahre auf den Rückfluss der Investitionskosten warten zu müssen. Andererseits gibt es aktuell, gerade aufgrund der gesetzlichen Vorgaben und immens gestiegener Strompreise, eine nie dagewesene Flut an potenziellen Investoren. Zusätzlich publiziert derzeit nahezu jeder Gigant der Branche schwindelerregende Zahlen bezüglich der geplanten Erweiterung von bestehenden Portfolios (1). Kurz gesagt: Der Handel mit Produktionsstätten für EE ist in aller Munde.

Aufgrund des enormen Ungleichgewichts im Markt, durch die Vielzahl an interessierten Käufern, tun sich viele Akteure schwer Assets zu erwerben. Dies bewirkt, dass viele Investoren opportunitätsgetrieben und ausschließlich einzelprojektbezogen inves­tieren. Dabei wird schnell deutlich, wie um­kämpft die Branche aktuell ist. Ein Umdenken auf Seiten der Käufer wird nötig, wenn die Renditeerwartung des Investors sich nicht mit der Kaufpreiserwartung des Verkäufers deckt und Investoren schlicht nicht konkurrenzfähig sind. Selbstverständlich kann teilweise auch mit Kriterien wie Trans­aktions­sicherheit etc. gepunktet werden, aber für viele Verkäufer zählt am Ende doch die bare Münze.

Dieses Umdenken findet im Markt aktuell statt, indem teilweise versucht wird, statt Einzelprojekten ganze Firmen, also Projektentwickler, zu erwerben, damit den Bewertungshorizont zu erweitern und zu hoffen, dass durch die Aussicht auf einen konstanten Strom an Neuprojekten attrak­tivere Angebote möglich sind und trotzdem die Renditeerwartungen gedeckt werden können.

Abgesehen davon gibt es noch weitere Ansätze, um die eigene Konkurrenzfähigkeit in diesem hart umkämpften Markt wieder­her­zu­stellen. Eine von diesen wird im folgendem etwas näher beschrieben. Es handelt sich um einen Perspektivenwechsel in der Betrachtung von EE-Portfolien. Dabei werden diese nicht nur als Summe ihrer Teile gesehen, sondern auch mögliche Syner­gie­effekte innerhalb eines Portfolios und die dadurch entstehenden positiven Effekte für den Investor berücksichtigt. Diese Effekte können sich dann im Kaufpreis manifestieren, um Investoren zu ermöglichen attraktivere Angebot abzugeben und somit die Kon­kurrenz­fähigkeit zu steigern.

Die Markowitz-Theorie

Die Grundlagen für den zu diskutierenden Ansatz bildet die Markowitz-Theorie, welche auch Portfolio-Theorie genannt wird. Dieses Konzept dürfte jeder Finanzökonom im Schlaf herunterbeten können, insbesondere, weil der „Erfinder“ Harry M. Markowitz im Jahre 1990 für seine Unternehmungen mit dem Wirtschafts-Nobel-Preis ausgezeichnet wurde. Der Ursprung der Theorie reicht bis ins Jahr 1952 zurück und gilt bis heute als Grundbaustein der modernen Portfolio-Theorie (2). Kurz gesagt beschäftigt sich die Theorie mit der Fragestellung, wie das Verlustrisiko durch die Schaffung von sogenannten effizienten Portfolien maximal reduziert werden kann, um somit bessere Renditen abzuwerfen, also genau das, was im EE-Markt gerade benötigt wird. Abbildung 1 zeigt die Anwendung der Theorie auf zwei fiktive Aktien.

Abbildung 1: Anwendung der Portfoliotheorie auf zwei fiktive Aktien nach Markowitz (3)

Beide Aktien weisen jeweils eine bestimmte Rendite (0,05 und 0,2 auf der Y-Achse) und einen Risikowert (0,015 und 0,025 auf der X-Achse) auf. Durch die Mischung beider Aktien in einem Portfolio bewegen sich Risikowert und Rendite entlang der dargestellten Linie. Der grün gekennzeichnete Bereich stellt den ineffizienten Teil dar, weil bei anderem Mischverhältnis für den gleichen Risikowert eine höhere Rendite existiert. Im mit MVP (Minimum-Varianz-Portfolio) markierten Punkt besteht das kleinstmögliche Risiko, während die rote Linie die maximale Rendite für jeden Risikowert darstellt.

Die Form der Kurve wird bestimmt durch den Grad der Korrelation beider Aktien zu­ein­an­der. Je mehr die beiden Aktien miteinander korreliert sind, desto mehr ähnelt die Kurve einer geraden Linie durch beide Punkte im Graphen. Deutlich wird jedoch, dass das Risiko durch die Mischung beider Aktien im Portfolio bei negativer Korrelation unter das Niveau der individuellen Betrachtung gesenkt werden kann. Darauf aufbauend ist es möglich, eine maximale Rendite für jeden im roten Bereich liegenden Risikowert einzustellen. Dies geschieht durch die Variation der Port­folio­zusammen­stellung.

Eine fast noch wichtigere Schlussfolgerung hier ist allerdings, dass bezogen auf die Rendite die Kombi­nation beider Aktien keinesfalls einer Mittel­wert­bildung beider Renditen gleich­kommt. Die Rendite kann durch negative Korrelation enorm gesteigert werden. Bei zwei perfekt korrelierten Aktien – also einer geraden Linie durch beide Punkte – würde sich bei einem Mischverhältnis von 50 % von Aktie A und 50 % von Aktie B eine Rendite von 0,125 bei einem Risiko von 0,2 einstellen. Durch die negative Korrelation ist im Beispiel bei demselben Risikofaktor von 0,2 eine Rendite von 0,175 möglich und es ergibt sich eine Steigerung um 40 %.

Dieses Prinzip kann mit beliebig vielen Aktien oder anderen wertgenerierenden Fi­nanz­instru­menten durch­geführt werden und ist somit eben­falls auf eine belie­bige An­zahl an EE-Projekten über­trag­bar, um entweder Ren­dite zu maxi­mieren oder das Risiko zu mini­mieren.

Anwendung auf EE-Projekte

Bei der Übertragung der Methodik auf den EE-Bereich muss zuerst ein Ziel der Analyse definiert werden. Fokus könnte hier neben vielen anderen Anwendungsfällen sein, eine ideale Zusammenstellung an Standorten für ein aufzubauendes Portfolio zu identifizieren. Es bleibt jedoch die Frage, wie es möglich ist, Assets im EE-Bereich effektiv qualitativ zu bewerten. Für jedes Projekt kann sowohl eine Erwartungsrendite als auch ein damit verbundenes Risiko bestimmt werden. Die tatsächlich eintretende Rendite und das vorhandene Risiko sind jedoch teilweise stark von externen Faktoren, wie z.B. der geo­politischen Lage oder der Störungs­freiheit der Anlagen abhängig. Diese Faktoren sind nicht oder nur wenig beeinflussbar, bestehen jedoch für alle Standorte gleichermaßen und können dementsprechend aus der Gleichung eliminiert werden. Zur Vereinfachung kann hier die Rendite mit dem Ertrag des Assets und das Risiko mit der Varianz dieses Ertrages am jeweiligen Standort gleichgesetzt werden. Im Bereich der Windenergie hat der Ertrag seinen Ursprung in der vor­herr­schenden Wind­geschwindig­keit. Im PV-Bereich wird der Ertrag haupt­sächlich durch die örtlich vor­herr­schende solare Ein­strahlung bestimmt.

Bei der Anwendung der Markowitz-Theorie an der Börse ist eines der Ziele die Zu­sammen­stellung von sogenannten effizienten Portfolien, bestehend aus verschiedenen Aktien, die möglichst perfekt negativ miteinander korrelieren und als „Hedge“ füreinander wirken. Bei der Betrachtung von Windenergie und Energie aus Photovoltaik kann auch ohne weitere Analysen festgestellt werden, dass beide Energie­gewinnungs­formen stark negativ korrelieren müssen und sich damit gut dazu eignen in einem Portfolio kombiniert zu werden.

Die Sonnen­ein­strahlung erreicht ihr Maximum in den Sommermonaten und ihr Minimum im Winter, während in den Wintermonaten die höchsten Wind­ge­schwindig­keiten gemessen werden und im Sommer eine Abschwächung des Windes messbar ist. Somit wird die Varianz im Portfolio bei Kombination beider Techno­lo­gien verringert, woraus sich ein konstanterer Ertrag ergibt. Bis hierhin werden weder Formeln noch komplexe mathe­ma­tische Modelle benötigt, um zu erkennen, dass ein Portfolio bestehend aus reinen Wind-Assets einen weniger konstanten Ertrag über den Verlauf eines Jahres bietet als ein Port­folio, dass beide Techno­logien kom­biniert.

Um Investoren tatsächlich bei der Auswahl zu erwerbender Assets zu unterstützen, muss dieser vereinfachte Ansatz jedoch aus­geweitet und zusätz­lich potenzielle Stand­orte ein­ge­bracht werden. Um eine Ab­schätzung zum Ertrag und der vor­herr­schenden Varianz an einem be­liebigen Ort abgeben zu können, muss auf histo­rische Wetter­daten zurück­ge­griffen werden.

Idealerweise sollten diese in einem mehrere Jahre umfassenden Betrachtungsfenster vorliegen, da insbesondere Wind­ge­schwindig­keiten nicht nur unterjährige saisonale Schwankungen, sondern auch zyklische Muster im Verlauf mehrerer Jahre aufweisen können. Glücklicherweise gibt es mittlerweile mehrere Anbieter, die solche historischen Wetterdaten öffentlich zu­gäng­lich machen.

Die Datengrundlage

Ein Beispiel für eine umfassende Erhebung historischer Wetterdaten ist die von der NASA publizierte Datenbank MERRA2. Hierbei handelt es sich um ein Projekt, mit welchem sich zum Ziel gesetzt wurde, so viele Reanalyse-Daten, wie möglich zu sammeln und bereitzustellen.

Die hauptsächlich mithilfe von Fernerkundung durch Satelliten erhobenen Daten haben eine weltweite Abdeckung mit einer Auflösung von ca. 50×50 km. Das heißt, dass damit ein weltweites Netz von Standortdaten vorhanden ist, bei dem ein Punkt nie mehr als 50 km vom nächsten Punkt entfernt ist. Die Historie dieser erfassten Standorte reicht bis ins Jahr 1980 zurück, während die Zeitreihe teilweise in stündlicher Auflösung zur Verfügung steht (4). Selbstverständlich entstehen dadurch riesige Datenmengen, die es zu bändigen gilt. Technisch können hier gängige Data-Science-Tools zum Einsatz kommen, um die Daten auf die gewünschte Art und Weise zu verarbeiten.

Die Analyse

Zur Einschätzung der Qualität wird anhand der historischen Daten für jeden betrachteten Standort ein mittlerer Ertrag und eine mittlere Standardabweichung (Varianz) berechnet. Die Varianz gibt dabei das Abweichungsrisiko von dem errechneten mittleren Ertrag an. Bei Bedarf kann der somit errechnete Ertrag zusätzlich mit einer Kostenkomponente versehen werden, damit beispiels­weise unter­schied­liche Investi­tions­kosten ver­schiedener Techno­lo­gien oder Er­richtungs­regio­nen/Län­dern berück­sichtigt werden.

Die Einheit der renditeseitigen Betrachtung verändert sich dementsprechend von produzierter Megawattstunde pro Jahr zu produzierter Megawattstunde pro inves­tiertem Euro und Jahr. Wird dieses Verfahren auf mehrere Standorte angewendet ergibt sich daraus ein Portfolio, das nach Markowitz optimiert werden kann. Abbildung 2 stellt beispielhaft ein solches Portfolio dar.

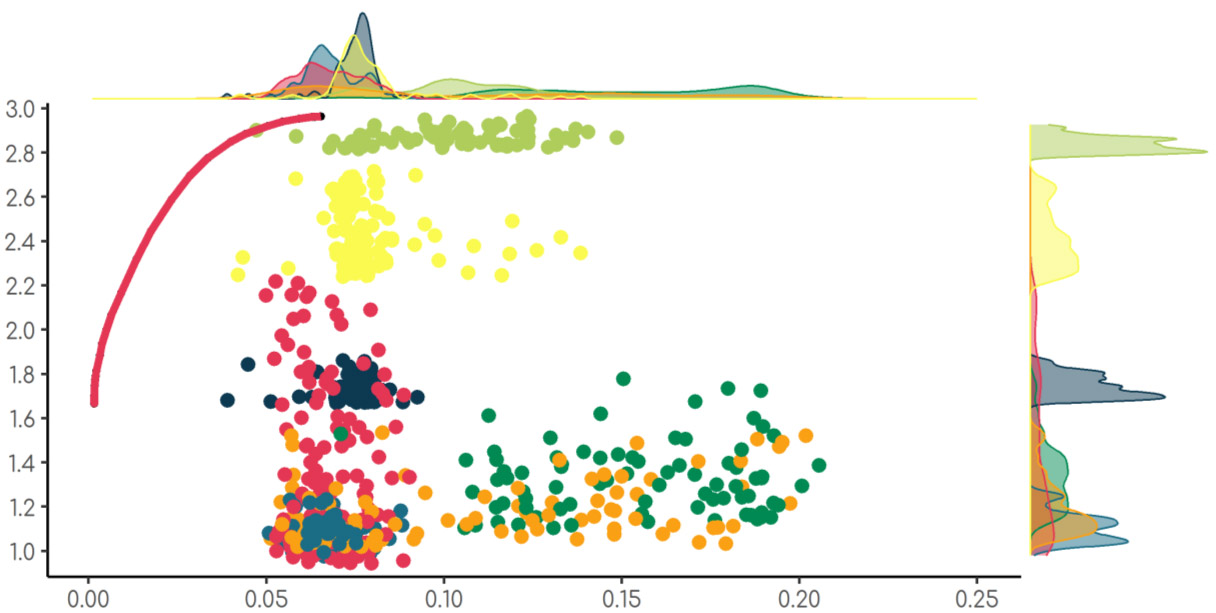
Abbildung 2: Beispielportfolioanalyse (eigene Darstellung)

Die einzelnen farbigen Punkte zeigen jeweils Standorte, die zur Zusammenstellung des Portfolios zu Verfügung stehen. Die rote Linie stellt den bereits aus Abbildung 1 bekannten effizienten Rand dar. Jeder Punkt auf dieser Linie steht somit für ein pareto-optimales Portfolio, für das weder Alternativen existieren, die die Rendite verbessern, ohne gleichzeitig das Risiko zu erhöhen, noch ein geringeres Risiko realisiert werden kann, ohne die Rendite zu verschlechtern.

Auch hier fällt auf, dass das Risiko be­zieh­ungs­weise das Ertrags­schwan­kungs­risi­ko bei Bedarf auf annähernd null reduziert werden kann. Dies liegt daran, dass in dem gewählten Beispiel über 5.000 Daten­punkte analy­siert wurden, unter denen sich viele nahezu perfekt negativ korre­lierte Bei­spiele be­finden.

Limitierende Faktoren

Damit ein aussagekräftiges Ergebnis entsteht, können der Analyse verschiedene limitierende Faktoren hinzugefügt werden. Durch die Limitierung der allokierbaren Kapazität an einem Standort, einer Region oder einem Land können die Ergebnisse verfeinert werden. Mithilfe dieser Einbindung eines solchen limitierenden Faktors können Umstände, wie begrenzte Verfügbarkeit an erwerbbaren Projekten, berücksichtigt werden. Weitere Ver­fei­nerungen könnten z.B. die Berück­sichti­gung des loka­len Strom­preises oder einer Fest­ver­gütung sein. Eben­falls denkbar wären Risiko­auf­schläge für die Re­präsen­tierung lokaler geo­poli­tischer Situa­tionen ein­zu­beziehen. Um ein be­steh­endes Port­folio sinnvoll zu er­wei­tern, könnten auch minimale Kapazi­täten an einem Stand­ort definiert werden, die dem Port­folio in jedem Fall bei­gemischt wer­den müssen und somit die be­reits be­steh­enden Pro­jekte reprä­sen­tieren.

Schlusswort

Schlussendlich bleibt die Frage zurück, warum eine solche veränderte, optimierte Be­trach­tung von Port­folien bisher kaum eine Rolle im EE-Bereich gespielt hat, obwohl durch die Ansätze für Fundmanager und sonstige Akteure der Börse längst zum Standard-Reparateure gehören. Eine mögliche Er­klä­rung könnte sein, dass viele Investoren nicht das Gefühl haben, wählerisch am Markt zu sein und deshalb rein oppor­tuni­täts­ge­trieben investieren. Dem gegenüber steht jedoch, dass, wie beschrieben, mit dieser Methode ebenfalls eine Optimierung der Gesamt­port­folio­rendite möglich ist, auch ohne gezielt Assets an be­stimm­ten Stand­orten zu er­wer­ben.

Eine weitere Erklärung könnte sehr schlicht sein und darin begründet liegen, dass es nicht nötig war solche Betrachtungen vor­zunehmen, da auch die Einzel­betrachtung der Assets bisher genug Wertsteigerung für alle involvierten Parteien generiert hat und man sich weiter­führen­dere Konzepte nicht bedienen musste, um erfolg­reich im Markt unterwegs zu sein. Dieser Trend scheint sich aktuell zu ändern und Investoren wird mehr abverlangt als noch vor einigen Jahren. Professiona­lität, Routine und erweiterte Kenntnis über den Wert des eigenen Assets der gesamten Branche auf der einen Seite und Kaufdruck im Markt durch zu viele Käufer schmählern die Renditen der Investoren und Verlagern die Wert­schöpfung weiter in Richtung der Verkäufer.

Sollten Sie als Investor diesen Druck auch spüren, sprechen Sie uns an und 4initia berät Sie gerne bezüglich einer Optimierung Ihrer bestehenden Portfolien oder Anpassung Ihrer Invest­ment­strate­gie, sodass Sie auch weiter­hin erfolg­reich im EE-Markt manö­vrieren können.

Autor: Yannick Sänger

QUELLEN:

(1) RWE AG (2022): 50 Milliarden Euro, 50 Gigawatt Kapazität bis 2030: RWE startet Investitions- und Wachstumsoffensive. Verfügbar unter: https://www.rwe.com/presse/rwe-ag/2021-11-15-rwe-startet-investitions-und-wachstumsoffensive (abgerufen am: 07.09.2022)
(2) Die moderne Portfoliotheorie nach Markowitz. Verfügbar unter: https://aktieninvestor.net/die-moderne-portfoliotheorie-nach-markowitz/ (abgerufen am: 07.09.2022)
(3) Portfoliotheorie. Verfügbar unter: https://de.wikipedia.org/wiki/Portfoliotheorie (abgerufen am: 07.09.2022)
(4) Global Modeling and Assimilation Office: Modern-Era Retrospective analysis for Research and Applications, Version 2. Verfügbar unter: https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/ (abgerufen am: 07.09.2022)